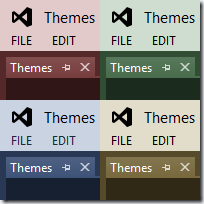
Visual Studio 2012 ships out of the box with 2 color themes, Light and Dark. Many users have complained the Light theme is too gray, depressing and ugly, some went as far as to claim they’d commit suicide if they’d be forced to look a whole day to this UI.
Personally I think that’s an exaggeration. However, while I absolutely like the Dark theme, and I could use the Light theme without problems, sometimes I’d prefer a bit more color.
For Visual Studio 2012 Professional/Premium/Ultimate there is a free Visual Studio 2012 Color Theme Editor extension that Matt Johnson wrote. It adds a couple color themes such as Red, Green, Blue, Purple, Tan, Dark with Light editor, Light with Dark editor. It also allows creating new themes, editing colors, etc.
Unfortunately, the extension is not available for Express editions of Visual Studio (and usually Express editions don’t allow loading extensions). It seems like on Express you’d be forced to use only the Light/Dark themes… Well, that’s not true!
Below I’ll tell you how to install the color themes on a Visual Studio 2012 Express, and I’ll exemplify with the newly released Visual Studio Express for Windows Desktop.
1) First, download the zip file http://www.alinconstantin.net/download/VS2012Themes.zip – it contains the 7 pkgdef files defining the colors of the default themes from Matt’s extension.
2) Now, create a folder under "%ProgramFiles%\Microsoft Visual Studio 11.0\Common7\IDE\WDExpressExtensions”, and lets name it “Themes”. Unpack the zip file in that folder.
3) Open a ‘Developer Command Prompt for VS2012” window. In the command line, type “wdexpress.exe /updateconfiguration”. This will make Visual Studio to read the pkgdef files on next restart, and import the color themes into registry.
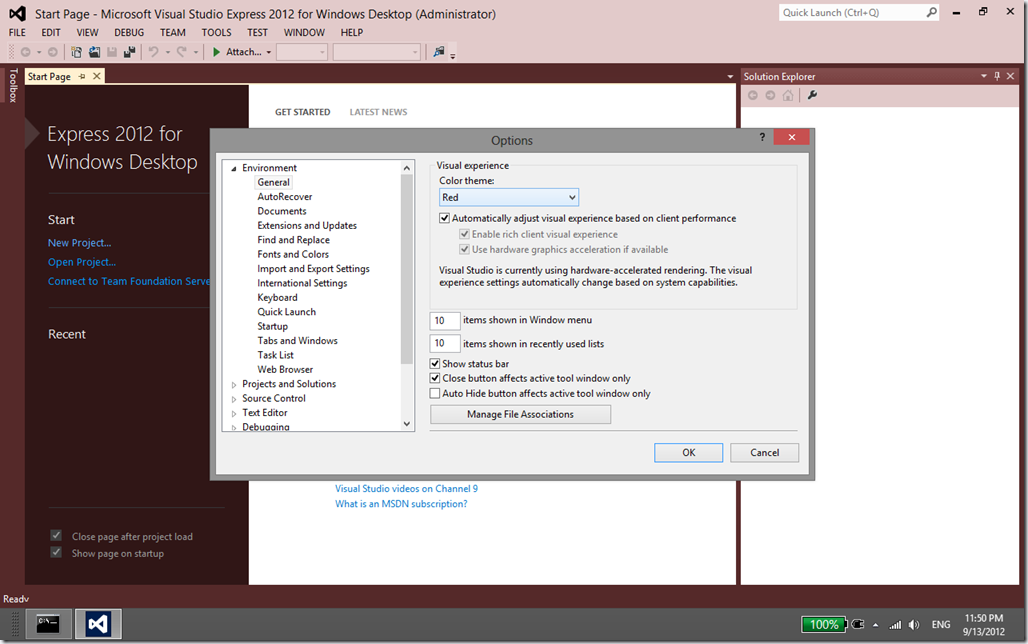
4) Launch Visual Studio Express, and now you should be able to see the new themes and switch them in Tools/Options dialog, Environment/General tab
Should someone with a VS Professional/Ultimate install use Matt’s extension to create/edit a custom theme that you want to use on Express, that’s also possible. On the machine with the VS install look under ‘%LocalAppData%\Microsoft\VisualStudio\11.0\Extensions’ folder. There should be some subfolders with random names, and one of them will contain a Colors.pkgdef file containing the theme of interest (open it with notepad and you should see in the beginning the theme’s name to confirm). Copy that file in the WDExpressExtensions\Themes folder, rename it to give it a more appropriate name (repeat steps 2-4), and you should be able to use the new custom theme.





71 comments:
Well done for that, Thanks!
Worked like a charm, thanks ;)
Also worked on Visual Studio 2012 Express RC for Windows 8.
Used: "%ProgramFiles(x86)%\Microsoft Visual Studio 11.0\Common7\IDE\VSWinExpressExtensions\"
and "vswinexpress.exe /updateconfiguration"
Great!
What about Visual Web Developer?
For Web Express, deploy to
"%ProgramFiles(x86)%\Microsoft Visual Studio 11.0\Common7\IDE\VWDExpressExtensions" and force the configuration update with "VWDExpress.exe /updateconfiguration"
Thank you very much Alin .
Great stuff, thanks so much. Now I can fiddle with code at home without feeling all suicidal and stuff.
Works great, thanks so much. Now I can fiddle with code at home without feeling all suicidal and stuff.
You are a hero among devs.
Very nice! Thanks.
Now it would be nice to have the bright blue bookmarks that were so easy to see in VS 2010.
Thanks a lot :) I just downloaded VS2012 today and thought both themes were really ugly but now i'm using the VS2010 style "Blue" theme and it's much nicer!
Excellent post. Works great in VS Express for Windows 8, but what about the Windows Phone 8 SDK? How do I get my themes into there?
@Captain Grogan:
Windows Phone 8 SDK contains another Express flavor of VS (aka VPDExpress)
So you can deploy the pkgdef files to "%ProgramFiles(x86)%\Microsoft Visual Studio 11.0\Common7\IDE\VPDExpressExtensions" and force the configuration update with "VPDExpress.exe /updateconfiguration"
Thanks, Alin, that works perfectly in the Windows Phone SDK.
Extremely useful, thanks! I thought I'm out of luck with Express edition.
Extremely useful post. I had been trying to change theme for Visual Web developer express edition since long time but without any luck. Default light and dark themes are so boring !!
Thank you very much !!
plz, do repair the link to alinconstantin.homeip.net/Download/...
@pcxp: The file is still there. Possibly when you tried the server rebooted, Comcast internet connection was down or the DNS server was not responding. You can also find the file in my website (alinconstantin.com/alinconstantin.net) in the Download section.
Thank you very much. Everything became very complex now... Impossible change color on IDE without installing command prompt and not manually editable configuration files.
Mais oui tu as raison ces couleurs noir ou blanche de base sont pourris lol. merci... Encore quelque jours d'installation et je pourrais peut etre compiler mes sources en x64
Merci ça marche super.
Thanks a lot!
Alin, thank you very much!
A few months ago when I first downloaded VS Wed Express 2012 I couldn't believe how bad the light and dark themes were. I searched in vain on the net to find a solution to no avail. But I hated using the standard themes so much I decided to search again today and I found your site. 15 minutes later I have a usable interface.
YTMND
Thank you very much!
From Russia with gratitude.
Thanks for posting this Alin! Those default themes were blinding me.
Thank you! Keep up the good work!
Thank you! Thank you!
Alin, has the VS2012Themes.zip file been moved? This is, quite literally, the only tutorial on changing the themes in VS Express. However, I cannot download the file. :(
Alin, has the VS2012Themes.zip file been moved? This is, quite literally, the only tutorial on changing the themes in VS Express. However, I cannot download the file. :(
@Mark: The file is still there.
The UPS battery failed and the damn thing decided to shutdown itself - my whole website was down. Sorry about that. It should be back now.
Until I replace the batteries, if the site goes down again try again later in a couple of hours..
Thanks, I was afraid I was going to need at least VS Professional for theming, but this works perfect.
Thanks for this. My colors in the editor window had suddenly become corrupted (text color from light theme with background color of dark theme for aspx files but not others...unreadable) But it did not work the first time because of 2 typos in your instructions. You said:
2) Now, create a folder under "ProgramFiles\Microsoft Visual Studio 11.0\Common7\IDE\WDExpressExtensions”
The last directory should be VWDExpressExtension and not WDExpressExtension. They both exist, just to make it confusing. Also, there is no Developer command prompt available in Express version, but the Windows command prompt works.
Finally, the command prompt should be “vwdexpress.exe /updateconfiguration” and not “wdexpress.exe /updateconfiguration”
It seems that my corrupted color configuration fixed itself just by running the updateconfiguration command (because I had installed the files in the wrong directory). But now I have other options!
@David: I don't think it's a mistake. It seems you're running Web Express and not Desktop Express. For Web Express, the name starts indeed with VWD (from the former name 'Visual Web Developer'), as I said in previous comments. For Desktop Express the name starts with just WD (from Windows Desktop). Confusing, I know.
Hi Alin,
Great post. I got it working, thanks alot.
I have a question. Are there any websites where people are making themes in the .pkgdef format and sharing them?
This website has some nice themes in the .vssettings format. Is there a way for Express users to convert them to .pkgdef?
http://studiostyl.es
@Anonymous: You don't need to convert the .vssettings files to .pkgdef format to use them. Just use the Tools/Import&Export settings to import the vssettings files (and the FontsAndColors values for the Editor will override those from the current Theme)
I'm not aware of websites publishing user themes.
yay!!! thank you
Hi
I am using VS 2012 Premium, i cannot open the Common7 using command prompt. Please advise how can i force the update. Or how to apply themes properly rather...
Anne
Hi
I am using VS 2012 Premium, i cannot open the Common7 using command prompt. Please advise how can i force the update. Or how to apply themes properly rather...
Anne
@Anne: If you have VS Premium you don't need this article - you can simply install Matt's extension from the VS Gallery (or Tools/ExtensionAndUpdates dialog)
thanks
Thanks a lot!
It works for my Visual Studio Express 2012 for Web
Multumesc Alin! ;)
thanks so much.. I couldn't stand either and within a matter of minutes of staring I was driven batty! Thanks for the hack :)
Thanks a million.
Thanks mate...You saved me ...colour does stimulate creativity in some...
Thanks mate...You saved me ...colour does stimulate creativity in some...
Thank you very much for posting this!
Awesome!
I know it worked for me on all the express versions. But has anyone an idea how to use this with the integrated shell Version?
Thanks man!
Does anybody have a solution for the "Visual Studio Express 2012 for Windows Phone" Edition?
There exists VPDExpress.exe but it doesn't have the parameter /updateconfiguration.
Any help would be great!
Awesome, thanks for this!
@anonymous: For VPDExpress, if you can't run /updateconfiguration (even though I see the flag being present in sources), you can run "VPDExpress /Setup" which will do full configuration rebuild, not just rebuild of pkgdef registrations.
perfeito.
Hello,
thanks for this site. It already helped me with the express version of VS for Desktop and VS for Windows 8.
The reason I post is, because I want to share my solution for the 2013 Preview. The express version seems to work the same way, but use the "Microsoft Visual Studio 12.0" directory instead of the "11.0".
The Custom Color Editor extension doesn't work in the Visual Studio 2013 Preview either, so installing Colors there works the same way:
Put the the pkgdef file in the folder: "…\Program Files (x86)\Microsoft Visual Studio 12.0\Common7\IDE\Extensions"
and then call "devenv /updateconfiguration" in the console.
Sincerely Martin
@Martin: For VS2013 the above solution will work only partially. There are new theme entries added in VS2013 that were not present in VS2012, and they aren't in the pkgdef files created for VS2012. When a color entry is missing from a theme VS will fallback to the Light theme colors, so if you use Purple theme and see colors that don't change, that is the reason. After VS2013 ships the Color Theme Editor will be released to target VS2013 so you should be able to create VS2013-specific pkgdef files.
Also, do NOT deploy the Blue.pkgdef in VS2013. Blue theme is now included in the box in VS2013, and has revised colors from the Blue theme shipped with the extension (or even with VS2012 Update2). If you deploy the VS2012 file you may get old colors or may fallback to Light for new color entries.
Unfortunately it seems the download-links domain is no longer alive. Would it be possible to put the file on dropbox or something?
Thanks.
@anonymous: Thanks for letting me know the website is inaccessible. It looks like I had a problem with dynamic DNS. I updated it now, should take a few hours to propagate (meanwhile you can access it via .com domain, as http://www.alinconstantin.com/download/VS2012Themes.zip )
Thanks to Alin Constantin for a helpful tutorial.
For those who don't have time ...
Here is a setup program I made for VS2012 Express that installs all of the color themes and update the VS configuration automatically for you.
here is the link for installer:
https://docs.google.com/file/d/0B3tn0GjiEnbfYlBfSU9ybFNvTzQ/edit?usp=sharing
I hope this helps,
Michael
It doesn't work for me as I get:VWDExpress.exe is not recognized as an internal or external command. I looked for it on my hard drive, but it isn't there. Any suggestions? Trying not to be suicidal!
@Anonymous: You must have VWDExpress.exe if you're running VS Express for Web (if you're running a different Express flavor, look for other binaries like WDExpress.exe, VsWinExpress.exe, VPDExpress.exe as it was pointed out in comments)
Look for it under your VS install folder under Common7\IDE subfolder.
Never mind, I got it to work. It was all under program file(x86) and I thought it was supposed to be under program files. It was your clue that VWDExpress must be running that got me on the right track. Thanks...much less suicidal now!
Still going strong - you rock for this...
Thank You Alin, it worked like a charm! BTW got here from the following link
[http://stackoverflow.com/questions/13149112/visual-studio-2012-express-desktop-color-theme-editor-extension]
Thank you Alin. Also worked on Visual Studio 2013 Express for Web (with the VWDExpress.exe binary)
Thank you Alin. Work fine with Visual Studio Express 2013 for Web also.
Thanks! Confirming this works for VSExpress 2013 as well.
Fantastic! Works like a charm!
Confirming this works on VSExpress 2013 for win 7 as well.
Alin, your tutorial works fine with the 2013 versions for Desktop and Web.
Thank you, very much!
Hi,
Thank you for this package. I just have a little issue: it works fine in my home computer but not in my office computer while I have downloaded exactly the same version: VS2012 express for Windows desktop. What may be the problem please?
Falimanana
Worked perfectly. Much appreciated!
Thank you very much, worked with /setup
Regards
What about Visual Studio Community Edition ? How would you go about installing it on that version if possible ?
Post a Comment